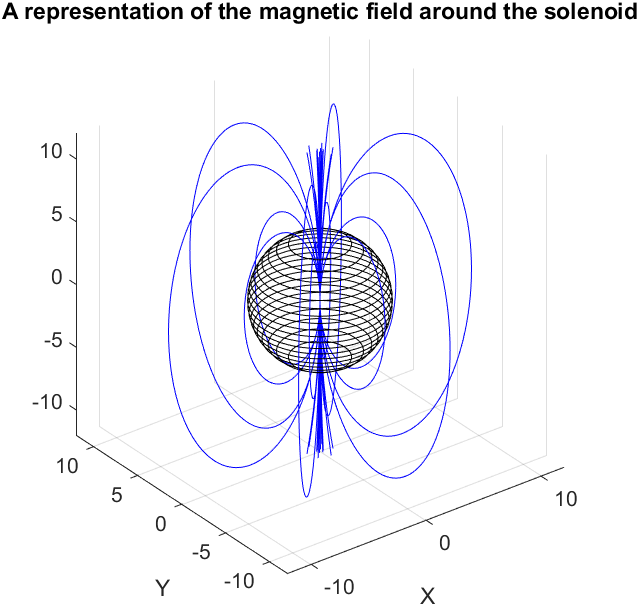
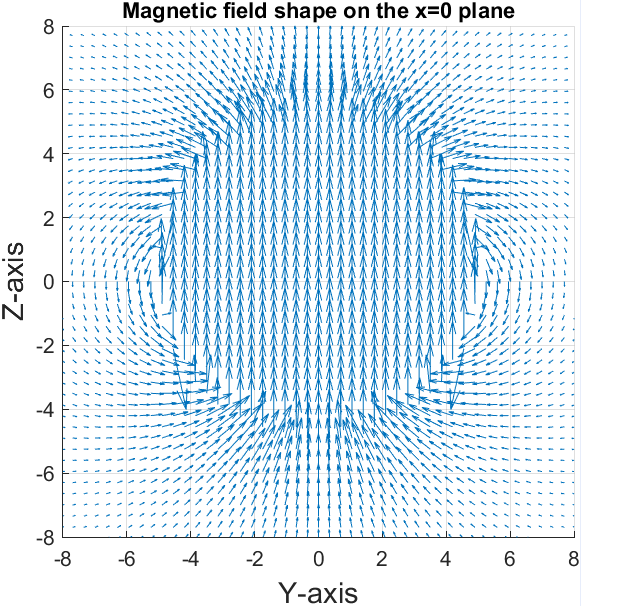
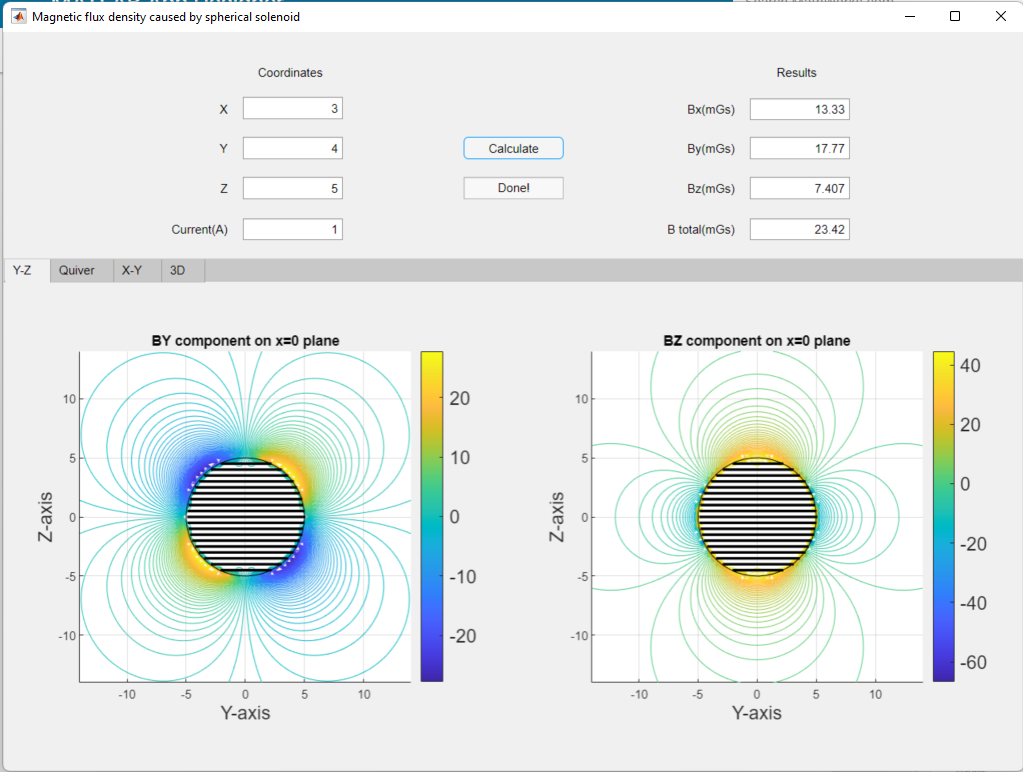
Magnetic Field Caused by a Spherical Solenoid
Spherical solenoid consists of current-carrying rings wound in parallel on a spherical core. To calculate the magnetic field resulting from the entire solenoid at an arbitrary point, the magnetic field resulting from each ring must be calculated and then by summing them, the total field at that point is calculated.
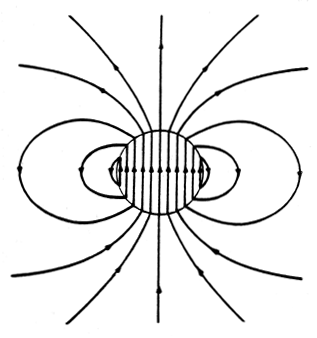
Magnetic field caused by a single ring of wire
According to the Biot–Savart law, the magnetic field caused by a single ring is $$\overrightarrow{B} = \frac{\mu_{0}I}{4\pi}\oint_{}^{}\frac{\overrightarrow{\ dl} \times \overrightarrow{R}}{|R|^{3}} .$$ Where \(\overrightarrow{R}\) is the displacement vector from the wire at point \(l\) to the point at which the field is being computed. We can define \(B\) as the radius of the solenoid thefore we can define \(b\) as the radius of the ring at height of \({z_{0}}\) from the solenoid's center. $$b = \sqrt{B^{2} - {z_{0}}^{2}}$$ We then define \({\overrightarrow{\ dl}}\) in the polar coordinates $$\overrightarrow{dl} = bd\varphi'{\widehat{a}}_{\varphi}$$ $$\overrightarrow{dl} = ( - b\sin(\varphi){\widehat{a}}_{x} + b\ cos(\varphi){\widehat{a}}_{y})d\varphi'$$ The displacement vector \(r\) is the distance from arbitrary point in space, \(P(r_{0},\theta_{0},\varphi_{0})\) , to the coordinates origin. $$ \overrightarrow{r} = r_{0}{\widehat{a}}_{r} + \theta_{0}{\widehat{a}}_{\theta} + \varphi_{0}{\widehat{a}}_{\varphi}$$ $$\overrightarrow{r} = r_{0}\sin\left( \theta_{0} \right)\cos\left( \varphi_{0} \right){\widehat{a}}_{x} + r_{0}\sin\left( \theta_{0} \right)\cos\left( \varphi_{0} \right){\widehat{a}}_{y} + r_{0}\cos\left( \theta_{0} \right){\widehat{a}}_{z} $$ Vector \(r'\) is defined as the displacement vector of \(dl\) to the coordinates origin as well. $$ \overrightarrow{r^{'}} = b{\widehat{a}}_{\rho} + \theta{\widehat{a}}_{\theta} + z_{0}{\widehat{a}}_{z}$$ $$\overrightarrow{r^{'}} = \sqrt{B^{2} - {z_{0}}^{2}}\cos(\varphi'){\widehat{a}}_{x} + \sqrt{B^{2} - {z_{0}}^{2}}\sin(\varphi'){\widehat{a}}_{y} + z_{0}{\widehat{a}}_{z} $$ By subtracting \()\overrightarrow{r}\) and \(\overrightarrow{r'}\) we can derive \(\overrightarrow{R}\), the displacement vector of point \(P(r_{0},\theta_{0},\varphi_{0})\) to the wire element \(dl\) $$\overrightarrow{R} = \overrightarrow{r} - \overrightarrow{r} \\ \\ \overrightarrow{R} = {\ (r}_{0}\sin\left( \theta_{0} \right)\cos{\left( \varphi_{0} \right) - \sqrt{B^{2} - {z_{0}}^{2}}\cos(\varphi'))}{\widehat{a}}_{x} + \\ \\ {\ (r}_{0}\sin\left( \theta_{0} \right)\sin{\left( \varphi_{0} \right) - \sqrt{B^{2} - {z_{0}}^{2}}\cos(\varphi'))}{\widehat{a}}_{y} + \\ \\ {(r}_{0}\cos\left( \theta_{0} \right) - z_{0}){\widehat{a}}_{z} $$ We can then calculate the absolute distance as $$|R| = \sqrt{\ ({r}_{0}\sin\left( \theta_{0} \right)\cos{\left( \varphi_{0} \right) - \sqrt{B^{2} - {z_{0}^{2}}}\cos(\varphi'))}^{2} + {(r_{0}\sin\left( \theta_{0} \right)\sin\left( \varphi_{0} \right) - \sqrt{B^{2} - {z_{0}}^{2}}\sin(\varphi'))}^{2}\ + {\ ({r}_{0}\cos\left( \theta_{0} \right) - z_{0})^{2}}} $$ At last, we derive the cross product of \({\overrightarrow{\ dl}}\) and \({\overrightarrow{\ R}}\) as $$ \overrightarrow{\ dl} \times \overrightarrow{R} = - \cos\left( \varphi^{'} \right)\sqrt{B^{2} - {z_{0}}^{2}}\left( z_{0} - r_{0}\cos\left( \theta_{0} \right) \right)d\varphi' {\widehat{a}}_{x} + \\ \\ - \sin\left( \varphi^{'} \right)\sqrt{B^{2} - {z_{0}}^{2}}\left( z_{0} - r_{0}\cos\left( \theta_{0} \right) \right)d\varphi' {\widehat{a}}_{y} + \\ \\ {( - \cos}{\left( {\varphi_{0} - \varphi}^{'} \right){r_{0}\sin}\left( \theta_{0} \right)}\sqrt{B^{2} - {z_{0}}^{2}} + B^{2} - {z_{0}}^{2}{)d\varphi' \widehat{a}}_{z}$$ With placing the derived expressions in the Biot–Savart Law Formula we can derive the magnetic field cause by a single ring at the height of \({z_{0}}\) at the point of \(P(r_{0},\theta_{0},\varphi_{0})\): $${\overrightarrow{B}}_{x} = \\ \\ \frac{\mu_{0}I}{4\pi}\int_{0}^{2\pi}{\frac{- \cos\left( \varphi^{'} \right)\sqrt{B^{2} - {z_{0}}^{2}}\left( z_{0} - r_{0}\cos\left( \theta_{0} \right) \right)d\varphi'}{ {|R|}^{3}}\ {\widehat{a}}_{x}} $$ $${\overrightarrow{B}}_{y} = \\ \\ \frac{\mu_{0}I}{4\pi}\int_{0}^{2\pi}{\frac{- \sin\left( \varphi^{'} \right)\sqrt{B^{2} - {z_{0}}^{2}}\left( z_{0} - r_{0}\cos\left( \theta_{0} \right) \right)d\varphi'}{ {|R|}^{3}}\ {\widehat{a}}_{y}} $$ $${\overrightarrow{B}}_{z} = \\ \\ \frac{\mu_{0}I}{4\pi}\int_{0}^{2\pi}{\frac{ {( - \cos}{\left( {\varphi_{0} - \varphi}^{'} \right){r_{0}\sin}\left( \theta_{0} \right)}\sqrt{B^{2} - {z_{0}}^{2}} + B^{2} - {z_{0}}^{2})\ d\varphi'}{ {|R|}^{3}}\ {\widehat{a}}_{z}} $$Generalization to all rings
If we assume the center of the sphere with radius of \(B\) is at coordinates origin, the height of the center of the parallel rings is between \(-B\) and \(B\). $$- B < z_{0} < B $$ Thus if we segment the sphere in to $n$ individual rings, the height of each ring would be $$ {z_{0}}_{i} = B - i\left( \frac{2B}{n} \right) \ \ \ \ \ \ i = 1,2,3,\ldots\ ,n$$ So the cumulative magnetic field of all rings would be $${\overrightarrow{B}}_{x_{total}} = \sum_{i = 1}^{n}{\overrightarrow{B_{x}}\left( {z_{0}}_{i} \right)} \\ \\ {\overrightarrow{B}}_{y_{total}} = \sum_{i = 1}^{n}{\overrightarrow{B_{y}}\left( {z_{0}}_{i} \right)} \\ \\ {\overrightarrow{B}}_{z_{total}} = \sum_{i = 1}^{n}{\overrightarrow{B_{z}}\left( {z_{0}}_{i} \right)} $$MATLAB Implementation
The derived formula was then implemented using MATLAB and the heatmap plot was calculated on multiple planes.